サ ンプルの[logic.lzh] をダウンロードしてください。解凍すると
[AND-OR.sio][Not.sio][XOR.sio]のファイルが作成されます。
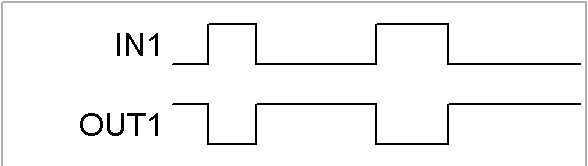
* サンプルの [Not.sio] を開 いてシミュレーションを実行してください。
[IN1] をONすると [OUT1] はOFFします。[OUT1] は [IN1] のインバータです。
[IN1] のOFFを [OUT1] のONの条件にして反転させます。OFFの条件は「ONの条件」がOFFする時に設定します。
 |
[IN1] がONしたとき出力がOFFします。 |
* サンプルの [AND-OR.sio] を開いてシミュレーションを実行してください。
[OUT1] は [IN1] と [IN2] の論理積(AND)出力です。ONの条件に「さらに」を選択してください。
[OUT2] は [IN1] と [IN2] の否定論理積(NAND)出力です。SiOには出力を反転させる機能がないので、[OUT1] のように
一度、論理積を作ってそれを[4-1.論理否定]で反転させるか、[OUT2] のようにド・モルガンの法則でプログラムします。
OUT2 = /[IN1] or /[IN2] = /( [IN1] and [IN2] )
[OUT3] は「複数選択」を使った例です。「複数選択」はOFFで使用すると、演算結果が否定されるのではなく入力が否定されます。
(■1.プログラミング時の注意点)を参照してください。
[OUT2] と同様に入力を否定したOR入力でNANDを実現します。
「複数選択2」をONで使用:[IN1] or [IN2]
「複数選択2」をOFFで使用:/[IN1] or /[IN2]
[OUT5] は [IN1] と [IN2] の論理和(OR)出力です。ONの条件に「または」を選択してください。
[OUT6] は [IN1] と [IN2] の否定論理和(NOR)出力です。ド・モルガンの法則でNORを実装しています。
OUT6 = /[IN1] and /[IN2] = /( [IN1] or [IN2] )
[OUT7] は「複数選択」を使った例です。SiOには演算結果を反転させて出力する機能がありません。
ド・モルガンの法則を使って入力側で演算結果を反転させる。
「複数選択」をOFFで使用すると、入力側が反転する。
* サンプルの [XOR.sio] を開 いてシミュレーションを実行してください。
[OUT1] は「複数選択1」をONとOFFで使用して排他的論理和を実装しました。
「複数選択1」は [IN1] と [FLAG1]( [IN2] の否定)の論理積です。「複数選択」の条件設定で「さらに」をチェックします。
「複数選択1」をON設定 「または」 「複数選択1」をOFF設定とすることで OUT1 = ( [IN1] and /[IN2] ) or ( /[IN1] and [IN2] )
としています。
[OUT2] は [FLAG] を使って排他的論理和を実装しました。
[FLAG2] = [IN1] and /[IN2]
[FLAG3] = /[IN1] and [IN2]
として OUT2 = [FLAG2] or [FLAG3] で実現しています。
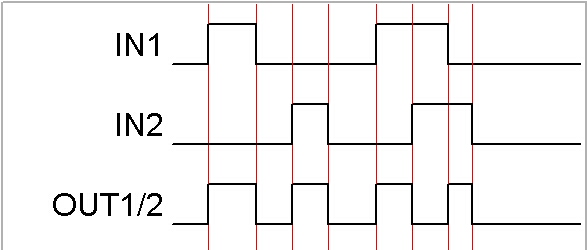 |
[IN1] と [IN2] のどちらかがONしたとき 出力がONしますが、入力が両方ONすると、 出力はOFFします。 |
[OUT4] は「複数選択2」をONとOFFで 使用して一致を作りました。「複数選択2」は[IN1] and [IN2] に設定しています。
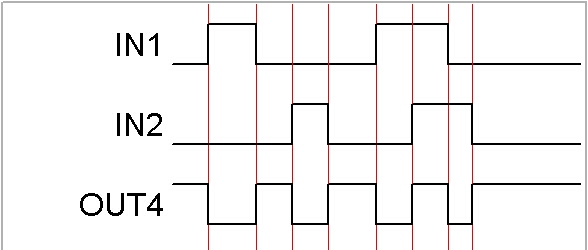 |
[OUT1] や [OUT2] の否定です。 [IN1] と [IN2] が一致したとき、 出力がONします。 |
「複数選択」をOFFで使用すると、入力側が反転する。
しかし「複数選択」の機能に否定入力が無いので、一度 [FLAG] を使って否定を作る必要がある。
(SUS株式会社様には「複数選択」の否定入力の機能追加を要望しています。)